Dalam kuliah fismat dipelajari bahwa jarak terpendek ialah garis lengkung menggunakan kuadrat elemen garis. Nah, sekarang akan saya ambil model lain dalam kehidupan nyata dan menjabarkannya menggunakan cara lain, astronomi bola. Sebelum membuktikan solusi dari problem ini, ada baiknya kita membahas terlebih dahulu mengenai astronomi bola.
Segitiga bola ialah segitiga yang dibentuk oleh busur-busur lingkaran besar. Yang dimaksud lingkaran besar ialah lingkaran yang berpusat pada pusat bola. Persamaan cosinus untuk segitiga bola ialah:
\begin{align} \cos a = \cos b \cdot \cos c + \sin b \cdot \sin c \cdot \cos A \label{cos} \end{align}Oke, kita akan membuktikan ini terlebih dahulu (kalau sudah tahu dilangkahi saja). Gambarkan segitiga bola (ABC) seperti di bawah ini, kemudian segitiga planar (ADE) sebagai proyeksi segitiga bola tadi. Ingat busur di depan sudut \(A\) diberi nama \(a\), dan seterusnya. Perhatikan bahwa \(\angle DAE = A\) dan \(\angle DOE = a\) .
Pada ΔDAE kita dapatkan:
\begin{align} \overline{DE}^2 = \overline{AD}^2 + \overline{AE}^2 - 2\overline{AD} \cdot \overline{AE} \cdot \cos A \label{p1} \end{align}Pada ΔDOE kita dapatkan:
\begin{align} \overline{DE}^2 = \overline{OD}^2 + \overline{OE}^2 - 2\overline{OD} \cdot \overline{OE} \cdot \cos a \label{p2} \end{align}Menyamakan persamaan (\ref{p1}) dengan (\ref{p2}), didapatkan
\begin{align} 2\overline{OD} \cdot \overline{OE} \cdot \cos a = (\overline{OD}^2-\overline{AD}^2)+(\overline{OE}^2-\overline{AE}^2) + 2\overline{AD}\cdot \overline{AE} \cdot \cos A \label{p3} \end{align}Sekarang perhatikan ΔDAO dan ΔOAE. Nampak dipenuhi jalinan:
\begin{align} \overline{OD}^2-\overline{AD}^2 &= \overline{AO}^2 \nonumber \\\overline{OE}^2-\overline{AE}^2 &= \overline{AO}^2 \nonumber \end{align}
Menyulihkan jalinan di atas ke dalam persamaan (\ref{p3}), menghasilkan
\begin{align} \overline{OD}\cdot \overline{OE}\: \cos a = \overline{AO}^2 + \overline{AD} \cdot \overline{AE}\: \cos A \nonumber \end{align}atau
\begin{align} \cos a=\frac{\overline{OA}}{\overline{OD}} \cdot \frac{\overline{OA}}{\overline{OE}}+\frac{\overline{AD}}{\overline{OD}} \cdot \frac{\overline{AE}}{\overline{OE}}\: \cos A \label{p5} \end{align}Pada ΔDAO, \(\frac{\overline{OA}}{\overline{OD}}\) ialah cosinus dari sudut \(\angle DOA\) dan \(\frac{\overline{AD}}{\overline{OD}}\) merupakan sinus dari sudut yang sama. Mengingat \(\angle DOA=c\), maka \(\frac{\overline{OA}}{\overline{OD}} = \cos c\) dan \(\frac{\overline{AD}}{\overline{OD}} = \sin c\). Begitu pula didapatkan \(\frac{\overline{OA}}{\overline{OE}} = \cos b\) dan \(\frac{\overline{AE}}{\overline{OE}} = \sin b\). Menyulihkan kesamaan-kesamaan ini ke dalam persamaan (\ref{p5}), diperoleh jalinan (\ref{cos}),
\begin{align} \cos a = \cos b \cdot \cos c + \sin b \cdot \sin c \cdot \cos A\nonumber \end{align}Nah, sekarang waktunya membuktikan jarak terpendek (geodesik) pada permukaan lengkung ialah garis lengkung pada proyeksinya. Perhatikan gambar.
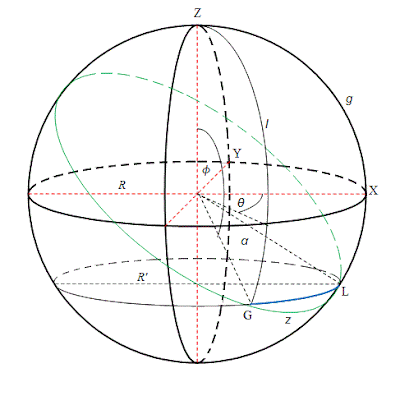
Misalkan kota Kentut (\(G\)) dan Sendawa (\(L\)) yang lintangnya hampir sama sekitar \(30^{\circ}\) Lintang Selatan dan bujur kota Kentut \(100^{\circ}\) BT sedangkan bujur kota Sendawa \(140^{\circ}\) BT. Kita dapatkan \(\phi = 90^{\circ} + 30^{\circ} = 120^{\circ}\) dan \(\theta = 140^{\circ} - 100^{\circ} = 40^{\circ}\). Dengan radius planet \(R=6371\) km, jika kita menempuh jalur lurus sepanjang lintangnya, maka didapatkan jarak
\begin{align} r_1 = \frac{\theta }{360^{\circ}}2\pi R'= \frac{\theta }{360^{\circ}}2\pi R\: \sin \phi \nonumber \end{align}Dengan memasukkan nilai didapatkan \(r_1 = 3851,9\) km.
Sekarang akan dihitung panjang lintasan geodesiknya. Jika kita menggunakan segitiga bola, maka sudut \(a\) ialah:
\begin{align} \cos a &= \cos \phi \: \cos \phi + \sin \phi\: \sin \phi\: \cos \theta \nonumber \\a &= \cos^{-1}\left ( \cos^2 \phi + \sin^2 \phi\: \cos \theta \right ) \nonumber \end{align}
Dengan demikian jarak kota Kentut dan kota Sendawa jika melalui lingkaran besar ialah
\begin{align} r_2 = \frac{a}{360^{\circ}}2\pi R \nonumber \end{align}Dengan memasukkan nilai didapatkan \(r_2 = 3831,6\) km, yang mana lebih pendek dari \(r_1\).
Jadi agar dapat menempuh jarak terpendek, alih-alih berjalan "lurus" sepanjang lintang, akan lebih pendek jika "berbelok" dulu ke selatan kemudian belok kembali ke utara.
Pustaka: Astronomy, Principle and Practice. A. E. Roy and D. Clarke.
Lihat juga:
Luna, Segitiga Bola, dan Teorema Girard.

bisa tau materi apa aja yg terkait di materi di atas gak??
BalasHapustrus ada solusi yg lain gak selain itu cara pembuktiannya??